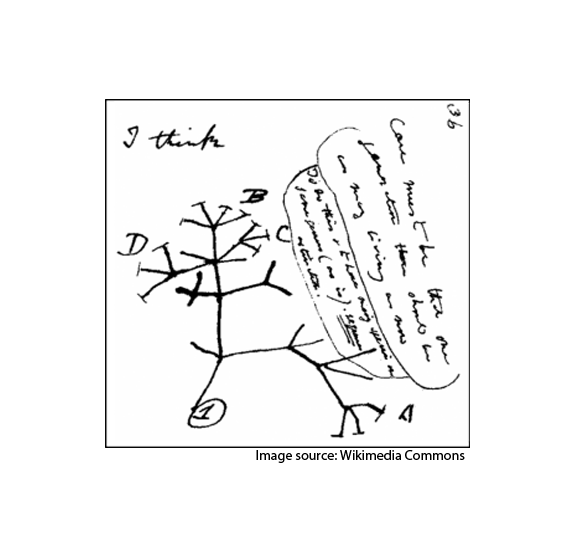
MEGA: Molecular Evolutionary Genetic Analysis
It is important to know the basic molecular relationship between two living organisms as one begins performing comparative studies for knowing the evolutionary aspects and for contributing to knowledge base. Several tools and soft ware have been introduced for meeting the task of such analysis. Each tool has different algorithm and method to perform molecular phylogeny. Examples include; ClustalW, Dendroscope, Hyphy, PAUP and Phylip etc. Among them is the most efficient tool, MEGA, Molecular evolutionary phylogenetic analysis which performs both sequence analysis and phylogenetic analysis in a very sophisticated manner.
MEGA’s functionality include the creation and exploration of sequence alignments, the enumeration of sequence divergence, the construction and visualization of phylogenetic trees, and the testing of molecular evolutionary hypotheses. Previously, many versions of MEGA had been released which integrate Web-based sequence data acquisition and their alignment capabilities with the evolutionary analyses. It makes comparative analyses much easier to conduct in a single computing environment. Over the period of time, this tool has come to boost up the classroom learning experience as its use by educators, researcher and students in different disciplines has expanded. This tool is contended with three distinct functionalities, along with some other features, which is why it is exercised for performing fine quality phylogenies by a large number of researchers and professionals as outlined below.
First, Caption Expert software module; generates descriptions for every result obtained by MEGA4. This enunciation informs the user about all of the options used in the analysis, including the data subset, the selected option for the handling of sites with gaps and missing data, the evolutionary model of substitution (e.g., nucleic acid substitution pattern, uniformity of evolutionary convergence or divergence and its rate among sites, and homogeneity or heterogeneity assumption among descendents, and the algorithms applied for estimating pair wise distances and for inferring and testing phylogenetic trees. The caption is also included with specific citations for any algorithm, method and software used in analysis. The availability of these descriptions is to promote a better understanding of the assumptions used in analyses, and of the results produced. This is needed because MEGA’s instinctive graphical interface makes it easy for both new and expert users to perform a variety of computational and statistical analyses. Sometime users don’t realize the underlying assumptions and data-handling options intricate in each analysis. Even expert population and molecular geneticists may not recognize all of the assumptions for immediate. Generally, a description of algorithm or method and results is useful for researchers and beginners when preparing tables and figures for presentation and publication.
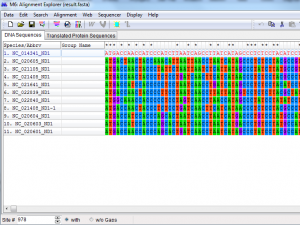
Second, Maximum Composite Likelihood (MCL) method is included for estimating evolutionary distances between nucleic acid sequences, which can be frequently employed by users for divergence times, inferring phylogenetic trees, and average sequence divergences between and within groups of sequences. In this approach, score is obtained as the sum of log likelihood for all sequence pairs in an alignment, and then is maximized by the common parameters for nucleotide substitution pattern to every sequence pair. This method was previously referred to as the ‘‘Simultaneous Estimation’’ (SE) method, because all distances are simultaneously estimated. This approach is different from current approaches for evolutionary distance estimation. In current approach, each distance is estimated independently of others, either by statistical formulas or by likelihood methods. The Maximum Composite Likelihood method has many advantages over the Independent Estimation (IE) approach. The IE method for estimating evolutionary distance for each pair of sequences often causes rather large errors unless very sequences are not estimated. One the hand, MCL reduces these errors, as a single set of parameter is applied to ever distance estimation. Inference of Phylogenetic trees by distance-based method is considered more accurate when error is low for estimation. This is in fact the case for the Neighbor-Joining method. The use of the MCL distances leads to a much higher accuracy with higher bootstrap values and even equal same topology of tree is expected to obtain. In addition, for pair wise distance calculation, IE method is not reliably applicable, because analytical formulas may become negative by chance due to algorithm’s arguments.
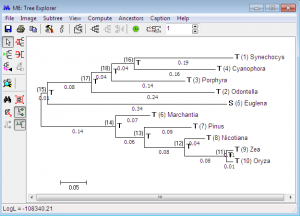
Such cases may increase with increase in number of sequence data, evolutionary distances become larger and substitution within sequences become more complex. The MCL method overcome these problems effectively and generates sophisticated models for inferring phylogenies from a larger number of diverse sequences. MEGA implicates the use of MCL method for evaluating average distances between and within groups, pair wise distances and average pairs, with their variances calculated by a bootstrap approach. The implementation of the MCL approach allows consideration of substitution rate variation from site to site, by an approximation of the gamma distribution divergence/convergence rates, and the assimilation of heterogeneity of nucleotide base composition in different sequences for species. We also have the leniency to determine the numbers of mutation per site separately. Intrinsically, the use of MCL method for inferring phylogenetic trees by distance-based methods, along with the bootstrap tests proves worth doing.